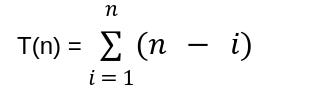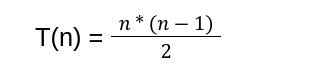A common sorting algorithm

Suppose, you have to sort a list of 100 numbers. How will you do it? There are many standard algorithms to do it. Let's talk about one such today. 

You pick up the first element in the list, and compare it with the remaining element of the list.

If the picked up element is greater than any of the elements it is compared with you do one swap operation i.e. you exchange the position of those two elements.

In a list of 100 numbers:

When you pick-up the 1st number, you do 99 comparison operations.

When you pick up the 2nd number, you do 98 comparison operations.

When you pick-up the 3rd number, you do 97 comparison operations.

You keep doing such till you reach the last element.

For the last element, there is no element left to be compared with i.e you do 0 comparison operations.

If you generalise this algorithm for *n* elements in the list, total number of comparison operations you need to do is

(n - 1) for the first element in the list.

(n - 2) for the second element in the list.

(n - 3) for the third element, and so on.

Considering, one comparison operation takes one unit time in a given machine:

We can derive the time function of this algorithm.

This is nothing, but the sum of consecutive numbers where the highest element is: (n - 1)

 So, the running time of this algorithm can be stated as: O ( n^2)

One thing you must notice is the number of swaps will always be less than or equal to the number of comparison operations i.e number of swaps can't be greater than number of comparison operations.

This algorithm is called selection sort.